Open-table formats such as Apache Iceberg, Delta Lake and Apache Hudi support analytic data sets on low cost, horizontally scalable storage.  The use of modern open-table formats on data lakes has been coined the term data lakehouse due to the aspiration of moving more of the traditional data warehouse workloads to the data lake.

Open-table formats introduce a metadata layer on top of files or objects. The table formats do not prescribe how data is organized into files, though. It is up to the application or engine executing a transaction against the table to create the files and determine their content. Such a design choice opens up for different ways to organize the data being added to a table into files. If we write n records into a table, then we can choose to split such records into 1, 10, 100 or 1000 files, arbitrarily or being smart about what data goes together in the same file.

The layout choice, although it may seem like a small detail, can have a very significant impact to the execution time of queries and consequently to compute costs. A poor data layout has a hidden cost, leading to a performance penalty that can be multiple times worse compared to a tuned choice.

Qbeast targets data layouts that enable an effective use of the optimization mechanisms available in query engines, inducing an efficient use of compute and storage resources. Our initial, short-term target is open-table formats and we plan to expand beyond such table formats to other data in the data lake over time. We presently focus on delivering efficient data layouts for lakehouse tables: data layouts that enable shorter execution times with the same resource configuration. It is critical to highlight that our focus is not purely on speed of execution, we ultimately want a data layout that brings compute costs to a minimum. Compute costs are increasingly an obstacle to the development and expansion of data projects and we support customers to overcome such costs.

‍

Lakehouse table data layout

We use data layout to denote the organization of the data of a lakehouse table across and within files. When we add data to a lakehouse table, we have the opportunity to choose what records go into which files — e.g., arbitrary vs. related values — and the organization within the files — e.g., naturally ordered vs. sorted — and different choices lead to different data layouts. Different layout choices lead to different query execution characteristics.

Having a desirable data layout requires understanding the mechanisms that modern distributed processing engines use to execute and optimize query execution. For example, data pruning using min-max values of table columns is a widely adopted technique to avoid reading data that is not relevant to a given query execution. Filtering, range selection, and even joins are examples of query operations that can largely benefit from data pruning. Reducing the intersection of min-max ranges across files and balancing file size and range width generally enables effective pruning.

Persisting min-max values as part of table metadata is not new and has been proposed in the context fine-grained data pruning structures such as zone maps [ZM] and small materialized aggregates [SMA]. Open table formats maintain stats such as min-max values per file to enable file skipping, e.g., stats in an addFile entry in the Delta Lake log, and a popular file format such as Parquet contains column stats at the granularity of row groups and data pages.

A natural approach to maximize the amount of data pruning with min-max values is to place similar data in the same file, reducing the overlaps of ranges across files and balancing file size and min-max range. Such clustering of records according to values is effective not only for data pruning but also for aggregations as data that needs to be aggregated, e.g., the sum of online purchases per customer id, is present in the same file, requiring less shuffling in a distributed execution.

‍

Using partitioning keys

A simple implementation of such grouping is to use a key, also known as partitioning key or clustering key, placing all records with the same key value in the same set of files. Such a key can be a single-column key or a compound key formed of values from multiple columns. As a simple example of a single-column key, if there is a date column with values ranging from “Jan 1st, 2025” through “Jan 31st, 2025”, then we can place all records with value “Jan 1st, 2025” in one or more files, all records with value “Jan 2nd, 2025” in one or more files, etc. Such an approach is often referred to as Hive-style partitioning in the context of data lakehouses due to the mechanism implemented in Apache Hive, a predecessor of modern table formats (see HIVE-936 for a detailed description of Hive dynamic partitions).

Partitioning keys are very commonly used because of its simplicity, its ability to evolve incrementally, and its effectiveness for workloads such as the ones involving time — e.g., partition data according to days or hours. Generally, partitioning can be problematic in the presence of high cardinality, though. If there are few records with a given key value, we end up with a lot of small files. We have the same problem when trying to partition using a compound key, we end up with an explosion on the number of partitions leading to small files. Say we have two columns each with 1,000 different values. In such a case, we have potentially 1,000,000 partitions.

‍

Clustering with multiple columns

When clustering data using multiple columns, it is desirable to be flexible about the grouping of data into files. Instead of being rigid and limiting to clusters of records with the same key value, we want to group records that are close. Being close hints at some notion of space and spatial locality. We can approach such a problem as a space defined by a subset of columns and we want to partition the space in a way that we balance data locality, file sizes and number of files.

The use of space-filling curves like Morton (Z-Order) [Morton] and Hilbert [Hilbert] curves for clustering has been gaining adoption for lakehouses to enable multi-dimensional clustering, e.g., for Iceberg and Delta Lake. The approach based on space-filling curves consists of deriving a single-dimension rank of records according to designated columns and partitioning this rank to determine the composition of files. The Morton Curve, for example, interleaves bits of the designated columns to derive such a rank per record.

Space-filling curves preserve spatial proximity: data points that are close in space are close in the single-dimension curve. Consequently, the use of such curves is suitable for multi-dimensional clustering. There are some important shortcomings of using space-filling curves, though:

• Deriving a single-dimensional curve out of multiple dimensions is a lossy process and there are anomalies observed in the order such as data points that are far in space being consecutive in the rank order.
• We have not spoken about tables that are regularly modified yet, but such a clustering method based on space-filling curves does not directly provide the means to evolve a table incrementally as we add data to it.
• Existing implementations induce a high overhead to the clustering, which can impact the execution such as ingesting new data into a table.

‍

Workload dependence

Of course, the choice of columns that are relevant for multi-dimensional clustering depends on the query workload. The designated columns are ideally referenced on a regular basis in queries in such a way that it can benefit from the clustered data layout. The coupling between designated columns and queries is weak, however, as queries are free to reference designated columns in different ways, e.g., filtering by different ranges, aggregating, etc.

A different approach to clustering is to use the workload to determine locality. Records that are expected to satisfy a given query predicate are clustered together. The approach taken by Amazon Redshift called MDDL is to use a multi-dimensional sort function to determine the sort order of records and cluster them accordingly [MDDL]. The sort function evaluates a record using relevant query predicates and returns a value indicating the predicates that it matches. This approach is effective with regular access to queries and constitutes a strict coupling between the clustering and the query workload, which suits well a closed data stack.

‍

Lakehouse table dynamics

The discussion this far does not take into account the fact that tables are very often not static. It is not that there is some amount of data that is generated once, and we have to organize the data layout once and never again. Lakehouse tables often evolve as new data is regularly generated and added or when data retention policies are applied. Example scenarios are the ones in which we are continuously ingesting telemetry data or user activity for analytics purposes.

As the table evolves, it is also critical to organize the data layout taking into account the previous clustering rounds. With partitioning, adding or deleting data is straightforward as changes affect whole partitions or subsets of files within partitions. Due to the limitation of partitioning for multi-dimensional clustering, we focus on options that enable clustering with multiple dimensions.

The approach using space-filling curves produces a single-dimension curve during a clustering round, but does not persist any structure that enables it to pick up the clustering from where it left off in future rounds. In principle, with space-filling curves, the clustering needs to be recomputed fully upon every change to the table. Of course, a practical implementation may choose not to recompute upon every change, and let the quality of the layout degrade, recomputing either on a regular cadence or when some condition is met.

One interesting and very important observation is that the degradation of the data layout is unavoidable when files are immutable and table changes affect the existing clustering. To illustrate, if we add new records to a table and these records are expected to be clustered with other existing records already part of the table, then either we have to re-write files to add the new records or we simply write new files with the new records only. In the latter case, the quality of the data layout degrades according to the clustering goal.

The practical impact of such degradation varies, and it tends to be small for a single table transaction, but it builds over multiple transactions. A typical approach to handle such degradation without having to resort to re-writes of files on each transaction is to have optimization cycles that re-write impacted files at arbitrary times or on a regular cadence. Without a structure to determine impacted files, it is difficult to cluster incrementally, typically requiring a re-computation of the clustering on such an optimization cycle, like with space-filling curves. Approaches such as Liquid Clustering — at least the open-source implementation — mitigates this problem by chunking the data into ZCubes and narrowing the optimization scope to a single ZCube, clustering incrementally. While it does avoid fully recomputing upon an optimization cycle, it also loses the ability of clustering globally as the scope of clustering becomes a ZCube.

‍

Using an index structure

Indexing is the concept of organizing information so that it can be quickly accessed. We can regularly find an index at the end of books, especially technical books, and generally in libraries. Book indexing has existed for centuries. For computer systems and databases, it has been used to speed up data retrieval and query execution. There are different types and ways to implement indices for a database depending on the particular set up and target application. For example, databases often use a tree-structured index like a B-Tree (and variants [B-Tree]) or an LSM-Tree while information retrieval systems use an inverted index. Spatial applications like GIS also use tree index structures such as Quad Trees [QuadTree], k-d Trees [k-dTree], R-Trees, etc.

Here we want to use an index structure in a different way. The primary goal is not to directly use the index to speed up the execution of queries. The primary goal is instead to build an index structure that enables us to identify blocks of data records that are part of the same logical clustering. As a table evolves, we want to quickly be able to both determine changes to the clustering on new transactions and identify files that need to be re-written when optimizing it, minimize the amount of re-writing during optimization while providing an efficient data layout.

For lakehouse tables, such an index structure is ideally stored with the table in a manner that is compatible with the underlying format, whether that is Apache Iceberg, Delta Lake or Apache Hudi, without inducing a new format. Such changes to the table are expected to be transparent to engines processing queries against the table, being visible only when updating the index. This approach is the one we pursue at Qbeast.

‍

The Qbeast way

Qbeast focuses generally on the data layout of data lakes, and has lakehouse tables using modern open-table formats as its immediate target. Open table formats such as Apache Iceberg, Delta Lake and Apache Hudi enable features such ACID transactions to modify tables, but they do not prescribe how data is organized across files. Qbeast benefits from this flexibility and provides a way to organize the data layout that is not tied to a specific table format or to a specific query engine.

Qbeast implements a multi-dimensional indexing approach for the data layout of lakehouse tables. It builds an index to guide the clustering of data, determining the content of the individual files written in a transaction. It takes a subset of designated columns of a table and projects records onto a space defined by the domains of the columns. The partitioning of this space induces an index tree structure that evolves with the table. It is based on the OTree index work [OTree] inspired by space partitioning techniques such as Quad Tree and k-d Tree.

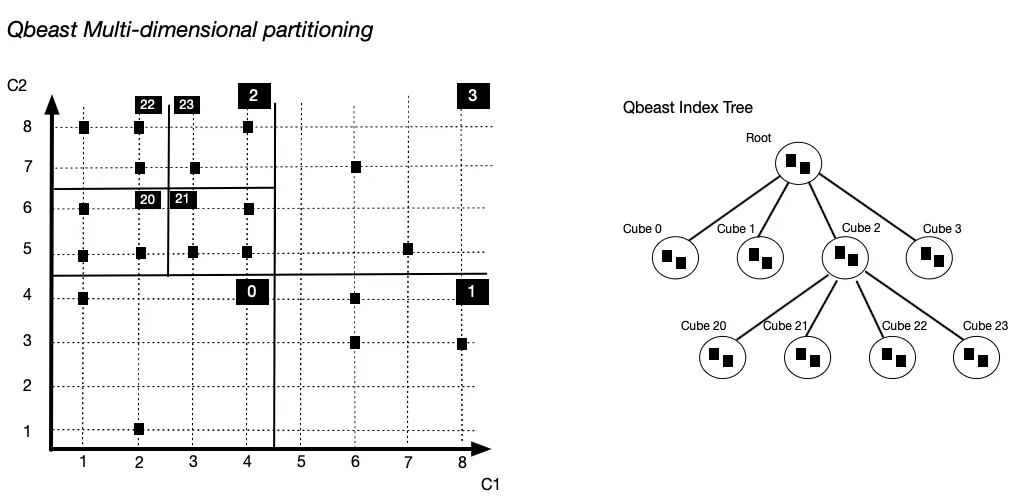
A Qbeast index tree is such that all tree nodes map to some part of the space that we call cube. Cube is a short for n-dimensional cube, for some number n of column dimensions. Each level of the tree corresponds to a refinement of the partitioning, e.g., the root maps to the whole space while its children map to the cubes corresponding to the first partitioning. A node of the tree contains a subset of the records contained in its corresponding cube. It is a subset because some records in the node subspace may map to an ancestor node or to a descendent node in the case it is not a leaf. In the illustration above, one record of Cube 1 maps to the root. This approach of mapping records to intermediate nodes enables the index tree to expand with the table while minimizing index and data layout changes.

The index tree is manipulated when performing a transaction against the table, whether that is an update to the table data or a re-write due to an optimization cycle, and we have an efficient way implemented of maintaining the index tree. The index is not used for query processing, except for the case of approximate queries. Queries that process a fraction of the data set can benefit from the index structure and read only a representative fraction.

When manipulating the index of a lakehouse table, we rely on an engine capable of executing transactions against the table. We presently use Apache Spark for this purpose and implement a library that contains the indexing logic used when indexing new or existing data, and when optimizing a table. The overall approach is not specific to Spark and can be ported to other engines.

The road ahead

As a product, we wrap the core indexing logic into a SaaS offer that enables customers to index and optimize lakehouse table data. We support all three main cloud providers — AWS, Google Cloud and Azure — and all three main open table formats — Apache Iceberg, Delta Lake and Apache Hudi. We have had some initial customer success with our approach with an observed reduction of the execution time of 79% and 98% less data read from storage, data read from storage. The future of Qbeast indexing will be driven by a mix of engineering insights, customer feedback and market input, and we expect to further enhance our lakehouse offer based on such feedback and to expand the scope of data layout to cover more scenarios beyond relational data, particularly focusing on supporting modern AI workloads.

Check this previous post for some additional detail on the Qbeast indexing and be on the lookout for new blogs elaborating on various topics about the technology we are developing. If you like our story and you want to be part of it, we are hiring.

‍

References

[B-Tree] Douglas Comer. 1979. Ubiquitous B-Tree. ACM Comput. Surv. 11, 2 (June 1979), 121–137. https://doi.org/10.1145/356770.356776

[Hilbert] J. K. Lawder and P. J. H. King. 2001. Querying multi-dimensional data indexed using the Hilbert space-filling curve. SIGMOD Rec. 30, 1 (March 2001), 19–24. https://doi.org/10.1145/373626.373678

[k-dTree] Jon Louis Bentley. 1975. Multidimensional binary search trees used for associative searching. Commun. ACM 18, 9 (Sept. 1975), 509–517. https://doi.org/10.1145/361002.361007

[MDDL] Jialin Ding et al., “Automated Multidimensional Data Layouts in Amazon Redshift”. In Companion of the 2024 International Conference on Management of Data (SIGMOD '24). Association for Computing Machinery, New York, NY, USA, 55–67. https://doi.org/10.1145/3626246.3653379

[Morton] Guy M. Morton, “A Computer-Oriented Geodetic Data Base and a New Technique in File Sequencing," International Business Machines (IBM), 1966

[LSM-Tree]  Patrick O’Neil, Edward Cheng, Dieter Gawlick, and Elizabeth O’Neil. 1996. The log-structured merge-tree (LSM-tree). Acta Inf. 33, 4 (Jun 1996), 351–385. https://doi.org/10.1007/s002360050048

[OTree] C. Cugnasco et al., "The OTree: Multidimensional Indexing with efficient data Sampling for HPC". In 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 2019, pp. 433-440, doi: 10.1109/BigData47090.2019.9006121.

[QuadTree] R. A. Finkel and J. L. Bentley. 1974. Quad trees a data structure for retrieval on composite keys. Acta Inf. 4, 1 (March 1974), 1–9. https://doi.org/10.1007/BF00288933

[SMA] Guido Moerkotte. 1998. Small Materialized Aggregates: A Light Weight Index Structure for Data Warehousing. In Proceedings of the 24rd International Conference on Very Large Data Bases (VLDB '98). Morgan Kaufmann Publishers Inc., San Francisco, CA, USA, 476–487.

[ZM] Mohamed Ziauddin, Andrew Witkowski, You Jung Kim, Dmitry Potapov, Janaki Lahorani, and Murali Krishna. 2017. “Dimensions based data clustering and zone maps”. Proc. VLDB Endow. 10, 12 (August 2017), 1622–1633. https://doi.org/10.14778/3137765.3137769